RBSE Solutions for Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Ex 5.2

RBSE Solutions for Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Ex 5.2

Rajasthan Board RBSE Class 12 Maths Chapter 5 Inverse of a Matrix and Linear Equations Ex 5.2

RBSE Solutions For Class 12 Maths Chapter 5 Question 1.
Find area of triangle, whose vertices are:
(i) (2, 5), (- 2, – 3) and (6,0)
(ii) (3, 8), (2, 7) and (5, – 1)
(iii) (0, 0), (5, 0) and (3, 4)
Solution:
(i) Area of triangle

(ii) Area of triangle

(iii) Area of triangle

RBSE Solutions For Class 12 Maths Chapter 5.2 Question 2.
Use determinant to find the area of triangle whose vertices are (1, 4), (2, 3) and (-5, – 3), Are these points collinear ?
Solution:
Area of triangle

These points are not collinear because area of triangle is not equal to zero.

Ex 5.2 Class 12 RBSE Question 3.
Find the value of k, if area of triangle is 35 sq. unit and vertices of triangle are (k, 4), (2, -6) and (5, 4).
Solution:
Given points (k, 4), (2, -6) and (5, 4) and area of triangle = 35 sq. unit

taking +ve sign
⇒ – 10k + 50 = 70
⇒ – 10k = 70 – 50
⇒ – 10k = 20
⇒ k = -2
taking -ve sign
– 10k + 50 = – 70
⇒ 10k = – 70 – 50
⇒ – 10k = – 120
⇒ k = 12
⇒ k= -2, 12.

RBSE Solutions For Class 12 Maths Chapter 5 Miscellaneous Question 4.
Use determinant to find k, if points (k, 2 – 2k), (-k + 1, 2k) and (-4 – k, 6 – 2k) and collinear.
Solution:
Given points (k, 2 – 2k), (-k + 1, 2k) and (-4 – k, 6 – 2k) are collinear.

⇒ k [2k – ( 6 – 2k)] – (2 – 2k) [(-k + 1) – (-4 – k)] + 1 [(-k + 1) (6 – 2k) – (-4 – k) (2k)] = 0
⇒ k [2k – 6 + 2k] – (2 – 2k) [-k + 1 + 4 + k ] + 1[- 6k + 2k² + 6 – 2k + 8k + 2k²] = 0
⇒ K(4k – 6) – (2 – 2k) (5) + 1(4k² + 6) = 0
⇒ 4k² – 6k – 10 + 10k + 4k² + 6 = 0
⇒ 8k² + 4k – 4 = 0
⇒ 2k² + k – 1 = 0
⇒ 2k ² + (2 – 1)k – 1 = 0
⇒ 2k(k + 1) – 1(k + 1) = 0
⇒ (k + 1) (2k -1)=0
Hence, k = -1, 1/2.

Exercise 5.2 Class 12 Solutions Question 5.
If point (3,-2), (x, 2) and (8, 8) are collinear, then find the value of x, using determinant.
Solution:
Given (3,-2), (x, 2) and (8, 8) are collinear.

⇒ 3(2 – 8) + 2(x – 8) + 1(8x -16) = 0
⇒ – 18 + 2x – 16 + 8x – 16=0
⇒ 10x – 50 = 0
⇒ 10x = 50
⇒ x = 50/10
Hence, x = 5

5.2 Class 12 Question 6.
Find the equation of line passing through the two points (3, 1) and (9, 3), using determinant, also find the area of traingle if third point is (– 2, – 4).
Solution:
Equation of line passing through (3, 1) and (93),
 
⇒ x(1 – 3) – (3 – 9) + 1(9 – 9) = 0
⇒ – 2x + 6 + 0 = 0
⇒ – 2(x – 3y) = 0
⇒ x – 3y = 0
Area of triangle

Area of triangle ∆ = 10 sq. unit (leaving -ive sign)

RBSE Solutions For Class 10 Maths Chapter 5.2 Question 7.
Solve the following system of equations by Cramer’s rule :
(i) 2x + 3y = 9, 3x – 2y = 7
(ii) 2x – 7y – 13 = 0, 5x + 6y – 9 = 0
Solution:
Given equations
2x + 3y = 9
3x – 2y = 7
Here,


Solution of equation be x = 3, y = -1.

Cramer’s Rule Class 12 Question 8.
Prove that following system of equation are inconsistent :
(i) 3x + y + 2z = 3
2x + y + 3z = 5
x – 2y – z = 1

(ii) x + 6y + 11 = 0
3x + 20y – 67 + 3 = 0
6y – 187 + 1 = 0
Solution:
Given equations
3x + y + 2z = 3
2x + y + 3z = 5
x – 2y – z= 1

= 3(- 1 + 6) – 1(-2 – 3) + 2 (- 4 – 1)
= 15 + 5 – 10 = 10 ≠ 0
∵ ∆ ≠ 0
∴ Solution is not possible.
Hence, system of equation are in consistent.
Hence proved.

(ii) Given equation
x + 6y + 11 = 0
or
x + 6y = – 11

3x + 20y – 6z + 3 = 0
or
3x + 20y – 6z = -3

6y – 18z = -1
Here


∵ ∆ = 0, ∆₁ ≠ 0, ∆₂ ≠ 0 and ∆₃ ≠ 0
∴ Solution of equations is not possible.
Hence, system of equation are inconsistent.
Hence proved.

Ex 5.2 Class 10 RBSE Question 9.
Solve the following system of equations by Cramer’s rule :
(i) x + 2y + 4z = 16
4x + 3y – 2z = 5
3x – 5y + z = 4

(ii) 2x + y – z = 0
x – y + z = 6
x + 2y + z = 3
Solution:
(i) Given equations
x + 2y + 4z = 16
4x + 3y – 2z= 5
3x – 5y + z = 4

(ii) Given equations
2x + y – z = 0
x – y + z = 6
x + 2y + z = 3

= 2(-1 – 2) – 1(1 – 1) – 1(2 + 1)
= -6 – 0 – 3 = -9

= 0(- 1 – 2) – 1(16 – 3) – 1(12 + 3)
= 0 – 3 – 15
= -18

= 2(6 – 3) – 0(1 – 1) – 1(3 – 6)
= 6 – 0 + 3
= 9

= 2(-3 – 12) – 1(3 – 6) + 0(2 + 1)
= -30 + 3 + 0
= -27
Using Cramer’s rule,

Hence, x = 2, y = -1, z = 3.

Exercise 5.2 Class 10 RBSE Question 10.
Solve the following system of equation using determinants :
(i) 6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8

Solution:
(i) Given equations
6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8

= 6(12 + 2) – 1(4 + 4) – 3(1 – 6)
= 84 – 8 + 15
= 91

= 5(12 + 2) – 1(20 + 16) – 3(5 – 24)
= 70 – 36 + 57
= 91

= 6(20 + 16) – 5(4 + 4) – 3(8 – 10)
= 216 – 40 + 6
= 182

= 6(24 – 5) – 1(8 – 10) + 5(1 – 6)
= 114 + 2 – 25
= 91

Using Cramer’s rule

Ex 5.2 Class 12 Question 11.
Use matrix method to solve following system of equations :
(i) 2x – y = -2
3x + 4y = 3

(ii) 5x + 7y + 2 = 0
4x + 6y + 3 = 0

(iii) x + y – 7 = 1
3x + y – 2z = 3
x – y – z = -1

(iv) 6x – 12y + 25z = 4
4x + 15y – 20z = 3
2x + 18y + 15z = 10
Solution:
(i) Given equations
2x – y = -2
3x + 4y = 3
Let AX = B

So, A^{– 1} exists.
On finding adjoint of matrix A
F₁₁ = 4, F₁₂ = -3, F₂₁ = 1, F₂₂ = 2
Matrix formed by adjoint of A,

(ii) Given equations
5x + 7y + 2 = 0 or 5x + 7y = -2
4x + 6y + 3 = 0 or 4x + 6y = – 3
⇒ AX = B …(i)

So, A^{– 1} exists.
On finding adjoint of matrix A,
F₁₁ = 6, F₁₂ = – 4, F₂₁ = – 7, F₂₂ = 5
Matrix formed by adjoint of A,

(iii) Given equations,
x + y – z = 1
3x + y – 2z = 3
x – y – z = -1
Let AX = B ……(i)

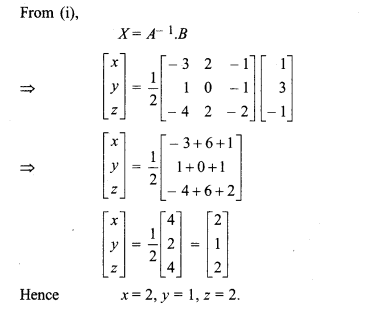
(iv) Given equations
6x – 12y + 25z = 4
4x + 15y + 15z = 3
2x + 18y + 15z = 10
AX = B ……….(i)

= 6(225 + 360) + 12(60 + 40) + 25(72 – 30)
= 3510 + 1200 + 1050 = 5760 = 0
So, A^{– 1} exists.
On finding adjoint of matrix A,

RBSE Solutions For Class 12 Maths Chapter 5.2 Question 12.
If img then, find A^{– 1} and solve the following system of linear equations :
x – 2y = 10,
2x + y + 3x = 8,
– 2y + z = 7
Solutin:
Given


= 1(1 + 6) + 2(2 – 0) + 0(- 4 – 0)
= 7 + 4 + 0
|A| = 11 ≠ 0
So, A^{– 1} exists.
On finding adjoint of A,

Matrix formed by adjoint of A,

Now, given equations
x – 2y = 10
2x + y + 3z = 8
– 2y + z = 7
In matrix form

RBSE Class 10 Maths Chapter 5.2 Question 13.
Find the product of matrices
  with the help of it, solve the following system of linear equations :
x – y + z = 4,
x – 2y – 2z = 9,
2x + y + 3z = 1
Solution:
Let


Matrix form of equations

Exercise 5.2 Class 12 Question 14.
Find the inverse matrix of matrix
 and with the help of it, solve the following system of equations :

Solution:

= 1(1 + 3) + 1(2 + 3) + 1(2 – 1)
= 4 + 5 + 1 = 10 ≠ 0
So, A^{– 1} exists.
On finding adjoint of A,

Matrix formed by adjoint of A,


Matrix form of equations

Class 12 Maths Ex 5.2 Question 15.
If (x₁, y₁), (x₂, y₂), (x₃, y₃) are vertices and a is side of an equilateral triangle respectively then prove that

Solution:

SabDekho

The Complete Educational Website

Bihar Board

UP Board

IAS Notes

Jac Board

MP Board

सम्पूर्ण व्याकरण

जीवनी

निबंध

टेन्स

सामान्य ज्ञान

Rajasthan Board

NCERT Solutions in Hindi

NCERT Solutions in English